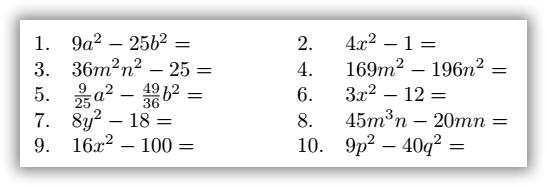FACTORIZACIÓN DE TRINOMIOS

FACTORIZACION  DE TRINOMIOS

 Factorizando Trinomios: x² + bx + c

 

Los trinomios de la forma x² + bx + c normalmente pueden factorizarse como el producto de dos binomios. Recuerda que un binomio es simplemente un polinomio de dos términos. Empecemos observando qué pasa cuando multiplicamos dos binomios, como (x + 2) y (x + 5).

 

 

Ejemplo
Problema	Multiplicar (x + 2)(x + 5).
	(x + 2)(x + 5)	Usa el método FOIL para multiplicar los binomios.
	x2 + 5x + 2x +10	Luego combina los términos semejantes 2x y 5x.
Respuesta	x2 + 7x +10

 

 

Factorizar es el reverso de multiplicar. Entonces vayamos en reversa y factoricemos el trinomio x² + 7x + 10. Los términos individuales x², 7x, y 10 no comparten factores comunes. Entonces vamos a reescribir x² + 7x + 10 como x² + 5x + 2x + 10.

 

Y, puedes agrupar los pares de factores:  (x² + 5x) + (2x + 10)

Factorizar cada par:                                    x(x + 5) + 2(x + 5)

Luego sacar el factor común x + 5:           (x + 5)(x + 2)

 

A continuación se muestra el mismo problema en la forma de un ejemplo:

 

Ejemplo
Problema	Factorizar x2 + 7x +10.
	x2 + 5x + 2x +10	Reescribe el término de en medio 7x como 5x + 2x.
	x(x + 5) + 2(x + 5)	Agrupa los pares y saca el factor común x del primer par y el factor 2 del segundo par.
	(x + 5)(x + 2)	Saca el factor común (x + 5).
Respuesta	(x + 5)(x + 2)

 

 

¿Cómo sabemos la manera de reescribir el término de en medio? Desafortunadamente, no puedes reescribirlo de una única manera. Si reescribes 7x como 6x + x, este método no funcionará. Afortunadamente, existe una regla para eso.

 

Factorizando Trinomios de la forma x2 + bx + c   Para factorizar un trinomio de la forma x2 + bx + c, encuentra dos enteros, r y s, cuyo producto sea c y cuya suma sea b.   Reescribe el trinomio como x2 + rx + sx + c y luego agrupa y aplica la propiedad distributiva para factorizar el polinomio . Los factores resultantes serán (x + r) y (x + s).

 

Por ejemplo, para factorizar x² + 7x +10, buscas dos números cuya suma sea 7 (el coeficiente del término central) y cuyo producto sea 10 (el último término).

 

Piensa en pares de factores de 10: 1 y 10, 2 y 5. ¿Alguno de ellos suman 7? Sí, 2 y 5. Entonces puedes reescribir 7x como 2x + 5x, y continuar factorizando como el ejemplo anterior. Observa que también puedes reescribir 7x como 5x + 2x. Ambas forman funcionan.

 

Factoricemos el trinomio x² + 5x + 6. En este polinomio, la parte b del término central es 5 y el término c es 6. Una tabla nos ayudará a organizar las posibilidades. A la izquierda, enlista todos los factores posibles del término c, 6; a la derecha encontrarás las sumas.

 

Factores cuyo producto es 6	Suma de los factores
1 • 6 = 6	1 + 6 = 7
2 • 3 = 6	2 + 3 = 5

 

Sólo hay dos combinaciones posibles de factores, 1 y 6, y 2 y 3. Puedes ver que 2 + 3 = 5. Entonces 2x + 3x = 5x, que nos da el término central correcto.

 Información Adicional

 

 

FACTORIZACION DE BINOMIOS

 Factorización de la diferencia de dos cuadrados

Una diferencia de cuadrados corresponde al tercer producto notable, en consecuencia para factorizar una diferencia de cuadrados se obtiene el producto de dos binomios donde el primer término de cada binomio será la raíz cuadrada del primer término y el segundo término de cada binomio corresponde a la raíz cuadrada del segundo término de la diferencia. Uno de esos binomios sumará sus términos, mientras el otro los restará.

 

Ejemplo

Factorizar 

Se calcula la raíz cuadrada de cada uno de los términos, obteniendo:

√9x2 =3x y √16y2 =4y

Luego la factorización será: 

9x2−16y2=(3x+4y)(3x−4y)

 

Ejercicios

Diferencia de cubos

Cualquier diferencia de cubos puede factorizarse de la siguiente manera:

1. Se extrae la raíz cubica del primer término y también del segundo.

2. Luego se escriben dos paréntesis el primero con la resta de las raíces y el segundo de la forma siguiente, la primera raíz al cuadrado más el producto de las dos raíces más el cuadrado de la segunda raíz, como se indica a continuación:

a3−b3=(a−b)(a2+ab+b2)

 

Ejemplo

Factorizar 

8−x3=(2−x)(22+2x+x2)=(4+2x+x2)